Sistemas numéricos

Desde la época prehistórica de la humanidad se ha tenido la necesidad de contar y medir, diversos autores refieren que el hombre comenzó a contar y medir antes de desarrollar la escritura, pero posterior al desarrollo del habla, se ha encontrado el uso de rudimentarios sistemas de numeración unarios, tallados en huesos u otros objetos.

La mayoría de las familias lingüísticas reflejan en sus sistemas numerales que la operación de contar estuvo asociado al conteo de dedos, por lo que esto sugiere porque muchas culturas utilizaron sistemas base decimal y vigesimal (contando todos los dedos de las extremidades) e incluso quinario (5), representados con una gran variedad de símbolos.

En el presente texto dejaremos de lado su representación gráfica, la cual siempre ha ido ligada a esta evolución y ha sido muy variada desde sus orígenes, según la sociedad que se estudie. En el presente texto se hará referencia a la notación posicional; en el que el sistema de numeración a cada dígito se le asigna un valor que depende de su posición relativa, la cual esta determinada por su base.

Actualmente, en gran parte del mundo, y en casi la mayoría de los casos se utilizan los números arábigos. Debido a su gran difusión y facilidad de uso, son utilizados para representar cantidades numéricas en diversas bases, eliminando algunos o incluso agregando letras para valores que no tienen representación numérica.

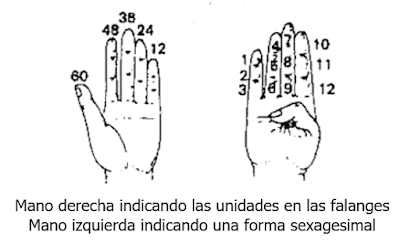
Un sistema utilizado aun en nuestros días es el duodecimal, es decir con base 12, se ha sugerido que inicio por la cantidad de falanges con las que cuenta una mano (solo 4 dedos, tal vez por eso en muchas caricaturas dibujen a los personajes con 4 dedos) y se utiliza el dedo pulgar como indicador para señalarlos. Como ejemplos se tiene: 12 meses, se pide una docena de artículos o media docena, una gruesa tiene 12 docenas (144 unidades), un pie tiene 12 pulgadas (pensaba que el rey era una persona deforme), una libra troy equivale a 12 onzas, etc.

Por otra parte, el sistema sexagesimal, con base 60, mide el tiempo o los ángulos (grados), como ejemplos se tiene: 60 segundos, 60 minutos.

Curiosamente estos sistemas (duodecimal y sexagesimal), pese a ser muy utilizados, no tienen un sistema de representación numérica propia o del estilo hexadecimal. Y para medir el tiempo se utiliza una base variable; los meses son 12, los días de la semana son 7, las horas de todo un día son 24, en teoría 12 de día y 12 de oscuridad. Una hora tiene 60 minutos, un minuto 60 segundos, y un segundo se divide en miles (diezmilésima de segundo).

Como se puede deducir la forma de contar ha cambiado en el transcurso de la historia, pero la necesidad sigue vigente y se siguen utilizando gran variedad de sistemas que facilitan los cálculos. Debido a la internacionalización, actualmente se puede considerar que el sistema numérico más utilizado en la vida diaria es el decimal, es decir de base 10. Como ejemplo tenemos nuestras monedas de intercambio, o diversas unidades de medida del “Bureau International des Poids et Mesures”.

El sistema decimal es un sistema numérico posicional, es decir está basado en la posición de los dígitos para establecer su valor, también se puede representar su valor como las potencias del número diez, sus valores numéricos van del 0 al 9, y este ciclo se repite nuevamente desplazando un espacio y sumando una unidad al digito desplazado. En este sentido estamos hablando cuando la unidad cambia a decena (cuando llega a nueve), y al completarse el ciclo de las decenas desplazamos otra posición para cambiar a centenas, y así sucesivamente de forma infinita.

Actualmente con el amplio uso de la electrónica digital, informática y ciencias de la computación, se utiliza el sistema binario, particularmente los dispositivos electrónicos (electrónica digital) en su forma más básica representan un estado de encendido o apagado o bit. El octal es utilizado para trabajar con bytes y conjuntos de ellos, donde un byte = 1 bit. Pero para que estos números “fácilmente entendidos por los dispositivos” sean más claros para los humanos se suele utilizar el hexadecimal, con base 16, que permite representar una palabra (word) con un dígito hexadecimales. 

Ejemplos de los sistemas numéricos más comúnmente usados:

Normalmente se utiliza un subíndice al final (del lado derecho) del numero para indicar la base a la que corresponde. En caso de no incluirlo se puede admitir que es base 10.

NOTA:

Los siguientes párrafos escapan un poco del tema de sistemas numéricos, pero considere interesante anexarlos (haga clic en leer más).

El sistema alfanumérico, con base 36, que utiliza para su representación los símbolos numéricos y alfabéticos latinos de la lengua inglesa (ignorando mayúsculas o minúsculas). Tiene algunas aplicaciones, aunque en informática no existe  natural que permita:

Wikipedia hace referencia a su uso para numerar patentes.

Otro sistema también utilizado, entre otros, es Base64, que permite la representación de los caracteres imprimibles ASCII. El codigo ASCII de cierta forma guarda cierta semejanza a los sistemas numéricos, aclarando que ASCII es un sistema de codificación de caracteres, por lo que no es lo mismo. Por otra parte, tocando ligeramente el tema de codificación de caracteres, existen diversas variantes de uso para el sistema binario y la representación numérica y alfanumérica, particularmente con aplicaciones en la electrónica digital y orígenes de las ciencias de la computación. Como los códigos de ocho bits, el código binario reflejado o código Gray, el código biquinario, el código 2 entre 5, Código Johnson, el Decimal codificado en binario (BCD), o el Código de intercambio decimal de código binario extendido (EBCDIC).

Fuentes Consultadas

 Becerra Espinosa (n/d) Sistemas de numeración. Página del Colegio de Matemáticas de la ENP-UNAM. Consultado en: http://dgenp.unam.mx/direccgral/secacad/cmatematicas/pdf/m4unidad02.pdf

COBALCH (n/d) Orígenes de algunos sistemas numéricos. Consultado en: http://lms.colbachenlinea.mx/tc-colbach/ScormViewer/tc-colbach/contenido/materias/01Primero/cvm1/scorm/11_orgenes_de_algunos_sistemas_numricos.html

ICMAT Communication (2018) Revoluciones Matemáticas - Capítulo 2: La conquista de los números. Video consultado en: https://www.youtube.com/watch?v=M44MdNSn788

Martin Malena (n/d) Historia de nuestros números. Aprendiendo matemáticas. Blog consultado en: https://aprendiendomatematicas.com/historia-de-nuestros-numeros-i/

Rodríguez Tamayo (n/d) Otros sistemas de numeración. CEIP Manuel Siurot. Andalucia, España. Recuperado de:
http://www.juntadeandalucia.es/averroes/centros-tic/21003232/helvia/sitio/upload/01___otros_sist_de_numer___apuntes.pdf

UnADM (2017) Unidad 1: Sistemas numéricos. Matemáticas discretas. Ciudad de México, México

Wikipedia (2020) Sistema numérico. Consultado en: https://es.wikipedia.org/wiki/Sistema_numérico